One turn loop coil

The inductance in the form of an isosceles triangle loop is calculated by the formula:

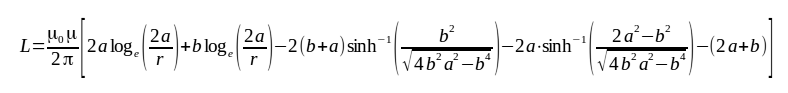
where:

• L - inductance [H];
• a, b - the sides of the triangle [m];
• r - radius of the wire (d/2) [m];
• μ₀ = 4π·10^-7 permeability of free space;
• μ - relative magnetic permeability of the conductor;

The inductance in the form of a rectangle loop is calculated by the formula: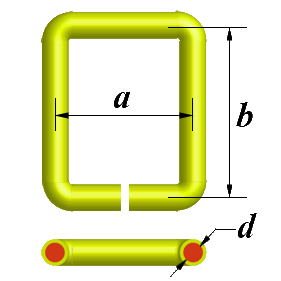

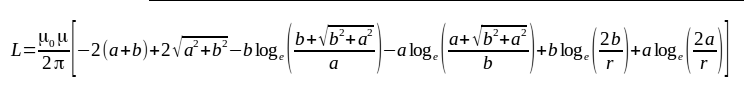
where:

• L - inductance [H];
• a, b - the sides of the rectangle [m];
• r - radius of the wire (d/2) [m];
• μ₀ = 4π·10^-7 permeability of free space;
• μ - relative magnetic permeability of the conductor;

The inductance in the form of a round loop is calculated by the formula:

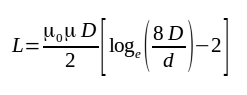
where:

• L - inductance [H];
• D - diameter of the loop [m];
• d - diameter of the wire [m];
• μ₀ = 4π·10^-7 permeability of free space;
• μ - relative magnetic permeability of the conductor;

You can often find the last formula in which the last member of the equation is 1.75 instead 2. That variant uses Coil32. In this case, the inductance of the round loop is calculated at high frequency. If the last term is 2, then the inductance is calculated at a low frequency. The low frequency means that the condition is met when the skin depth is greater than the wire radius. At the high frequency the skin depth is much less than the wire radius.

References:

• Inductance Calculations: Working Formulas and Tables - © F W Grover, 1946 and 1973. Dover Phoenix Edition 2004. ISBN: 0 486 49577 9.2009 reprint ISBN13: 9780486474403