Toroidal inductor calculation

Toroidal coils without a magnetic core are used very rarely. The magnetic field of a coil is almost completely centered inside of the toroid, with this kind of design has a low stray field and, accordingly, this coil is little affected by external fields even without a shield. To calculate the inductance of a toroid of circular cross-section we can take the formula for calculating the inductance of the solenoid (formula[2]). S should be replaced by the cross-sectional area of the toroid and l is the average length of the circumference of the toroid.
| [1] |
Where A is the cross-sectional area of the toroid and the R is the average radius of the circumference of the toroid, μ0 is the magnetic constant. Inductance is in Henry, dimensions are in meters.
The more practical formula that coil64 uses: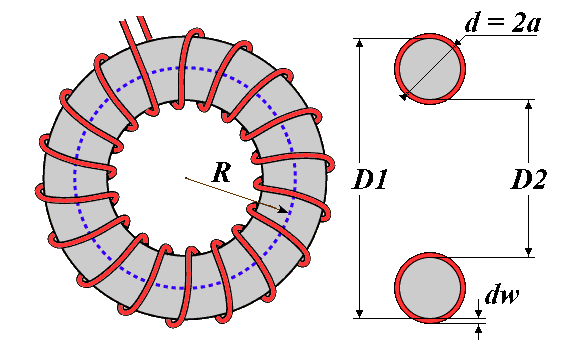
| [2] |
Inductance in micro Henry, dimensions are in centimeters, N is the number of turns of the coil, R is the average radius of the circumference of the toroid, a is the winding radius. The formula can be used for practical calculations of the toroidal air core coils with round cross section. The additional formulas:Where D1 D2 are the outer and the inner diameters of the toroidal coil-former, dw is the wire diameter.

However, in Amateur radio practice, we often deal with toroids having a square cross section, although with a large number of turns, the cross-section of a coil becomes more look like an ellipse. Experimentally it was found, that in case of the toroid with a square cross section, it is better to use empirical formulae for coil on a ferrite ring, only the permeability in this case is equal to one. It is implemented in the program Coil64.










